Conditional Probability for Sports Betting 1

Conditional probability is a fundamental concept in probability theory that deals with the probability of an event occurring given that another event has already occurred. It’s an important tool for understanding the relationship between two events, which as you can imagine is incredibly useful for sports betting parlays.

Definition and Formula

The conditional probability of an event A given that event B has occurred is denoted as: $P(A|B)$

This is read as “the probability of A given B”. The formula for conditional probability is:

$P(A|B) = \frac{P(A \cap B)}{P(B)}$

Let’s break this down by it’s parts:

$P(A \cap B) :$ the probability that both events A and B occur

$P(B):$ the probability of event B.

Intuition and Examples

Coin Toss: Suppose you toss a fair coin twice. The probability of getting heads on the second toss, given that the first toss was heads, is simply the probability of getting heads on a single toss, which is 0.5. This is because the two events are independent.
Drawing Cards: Imagine you have a deck of cards (52 cards total). The probability of drawing an Ace is 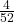$\frac{4}{52} \)$ Now, suppose you drew a card and it’s a King. The conditional probability of drawing an Ace next, given that you’ve already drawn a King, changes because there are now 51 cards left, so it becomes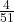 $\frac{4}{51} \)$

Independent and Dependent Events

Independent Events: If two events are independent, the occurrence of one does not affect the probability of the other. In this case, $P(A|B) = P(A) \)$
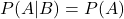
Dependent Events: If events are dependent, the occurrence of one event affects the probability of the other. In the card example, the events are dependent because the outcome of the first draw affects the second.

The Multiplication Rule

Conditional probability is related to the multiplication rule:

$P(A \cap B) = P(A|B) \times P(B)$

This formula is used to find the probability of both A and B occurring.

Real-World Applications BESIDES Sports Betting

Medical Diagnosis: Estimating the likelihood of a disease given certain symptoms.
Machine Learning: In classification problems, calculating the probability of a class given the features.
Finance: Assessing the probability of investment risks given market conditions.

In summary, conditional probability is crucial for understanding how the likelihood of events changes when we have additional information. It’s a key tool in statistical inference and decision-making processes.